Suffix array
In computer science, a suffix array is an array of integers giving the starting positions of suffixes of a string in lexicographical order.
Contents |
Details
Consider the string
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| a | b | r | a | c | a | d | a | b | r | a | $ |
of length 12, that ends with a sentinel letter $, appearing only once, and less (in lexicographical order) than any other letter in the string.
It has twelve suffixes: "abracadabra$", "bracadabra$", "racadabra$", and so on down to "a$" and "$" that can be sorted into lexicographical order to obtain:
| index | sorted suffix | lcp |
|---|---|---|
| 12 | $ | 0 |
| 11 | a$ | 0 |
| 8 | abra$ | 1 |
| 1 | abracadabra$ | 4 |
| 4 | acadabra$ | 1 |
| 6 | adabra$ | 1 |
| 9 | bra$ | 0 |
| 2 | bracadabra$ | 3 |
| 5 | cadabra$ | 0 |
| 7 | dabra$ | 0 |
| 10 | ra$ | 0 |
| 3 | racadabra$ | 2 |
If the original string is available, each suffix can be completely specified by the index of its first character. The suffix array is the array of the indices of suffixes sorted in lexicographical order. For the string "abracadabra$", using one-based indexing, the suffix array is {12,11,8,1,4,6,9,2,5,7,10,3}, because the suffix "$" begins at position 12, "a$" begins at position 11, "abra$" begins at position 8, and so forth.
The longest common prefix is also shown above as lcp. This value, stored alongside the list of prefix indices, indicates how many characters a particular suffix has in common with the suffix directly above it, starting at the beginning of both suffixes. The lcp is useful in making some string operations more efficient. For example, it can be used to avoid comparing characters that are already known to be the same when searching through the list of suffixes. The fact that the minimum lcp value belonging to a consecutive set of sorted suffixes gives the longest common prefix among all of those suffixes can also be useful.
Algorithms
The easiest way to construct a suffix array is to use an efficient comparison sort algorithm. This requires 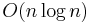 suffix comparisons, but a suffix comparison requires
suffix comparisons, but a suffix comparison requires 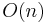 time, so the overall runtime of this approach is
time, so the overall runtime of this approach is 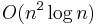 . More sophisticated algorithms improve this to
. More sophisticated algorithms improve this to 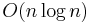 by exploiting the results of partial sorts to avoid redundant comparisons. Several
by exploiting the results of partial sorts to avoid redundant comparisons. Several 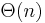 algorithms (of Pang Ko and Srinivas Aluru, Juha Kärkkäinen and Peter Sanders, etc.) have also been developed which provide faster construction and have space usage of
algorithms (of Pang Ko and Srinivas Aluru, Juha Kärkkäinen and Peter Sanders, etc.) have also been developed which provide faster construction and have space usage of 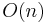 with low constants. These latter are derived from the suffix tree construction algorithm of Farach.
with low constants. These latter are derived from the suffix tree construction algorithm of Farach.
Recent work by Salson et al. proposes an algorithm for updating the suffix array of a text that has been edited instead of rebuilding a new suffix array from scratch. Even if the theoretical worst-case time complexity is 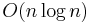 , it appears to perform well in practice: experimental results from the authors showed that their implementation of dynamic suffix arrays is generally more efficient than rebuilding when considering the insertion of a reasonable number of letters in the original text (Léonard, Mouchard and Salson).
, it appears to perform well in practice: experimental results from the authors showed that their implementation of dynamic suffix arrays is generally more efficient than rebuilding when considering the insertion of a reasonable number of letters in the original text (Léonard, Mouchard and Salson).
Applications
The suffix array of a string can be used as an index to quickly locate every occurrence of a substring within the string. Finding every occurrence of the substring is equivalent to finding every suffix that begins with the substring. Thanks to the lexicographical ordering, these suffixes will be grouped together in the suffix array, and can be found efficiently with a binary search. If implemented straightforwardly, this binary search takes 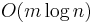 time, where
time, where  is the length of the substring W. The following pseudo-code from Manber and Myers shows how to find W (or the suffix lexicographically immediately before W if W is not present) in a suffix array with indices stored in pos, starting with 1 as the first index.
is the length of the substring W. The following pseudo-code from Manber and Myers shows how to find W (or the suffix lexicographically immediately before W if W is not present) in a suffix array with indices stored in pos, starting with 1 as the first index.
if W <= suffixAt(pos[1]) then
ans = 1
else if W > suffixAt(pos[n]) then
ans = n
else
{
L = 1, R = n
while R-L > 1 do
{
M = (L + R)/2
if W <= suffixAt(pos[M]) then
R = M
else
L = M
}
ans = R
}
To avoid redoing comparisons, extra data structures giving information about the longest common prefixes (LCPs) of suffixes are constructed, giving 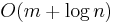 search time.
search time.
Suffix sorting algorithms can be used to perform the Burrows–Wheeler transform (BWT). Technically the BWT requires sorting cyclic permutations of a string, not suffixes. We can fix this by appending to the string a special end-of-string character which sorts lexicographically before every other character. Sorting cyclic permutations is then equivalent to sorting suffixes.
Suffix arrays are used to look up substrings in Example-Based Machine Translation, demanding much less storage than a full phrase table as used in Statistical machine translation.
History
Suffix arrays were originally developed by Gene Myers and Udi Manber to reduce memory consumption compared to a suffix tree. This began the trend towards compressed suffix arrays and BWT-based compressed full-text indices.
References
- Udi Manber and Gene Myers (1991). "Suffix arrays: a new method for on-line string searches". SIAM Journal on Computing, Volume 22, Issue 5 (October 1993), pp. 935–948.
- Pang Ko and Srinivas Aluru (2003). "Space efficient linear time construction of suffix arrays." In Combinatorial Pattern Matching (CPM 03). LNCS 2676, Springer, 2003, pp 203–210.
- Juha Kärkkäinen and Peter Sanders (2003). "Simple linear work suffix array construction." In Proc. 30th International Colloquium on Automata, Languages and Programming (ICALP '03). LNCS 2719, Springer, 2003, pp. 943–955.
- M. Farach (1997). "Optimal Suffix Tree Construction with Large Alphabets". FOCS: 137–143.
- Klaus-Bernd Schürmann and Jens Stoye (2005). "An incomplex algorithm for fast suffix array construction". In Proceedings of the 7th Workshop on Algorithm Engineering and Experiments and the 2nd Workshop on Analytic Algorithmics and Combinatorics (ALENEX/ANALCO 2005), 2005, pp. 77–85.
- Mikaël Salson, Martine Léonard, Thierry Lecroq and Laurent Mouchard (2009) "Dynamic Extended Suffix Arrays", Journal of Discrete Algorithms 2009.
- Martine Léonard, Laurent Mouchard and Mikaël Salson (2011) "On the number of elements to reorder when updating a suffix array", Journal of Discrete Algorithms, 2011.
External links
- Various algorithms for constructing Suffix Arrays in Java, with performance tests
- Suffix sorting module for BWT in C code
- Suffix Array Implementation in Ruby
- Suffix array library and tools
- Project containing Suffix Array Implementation in Java
- Project containing various Suffix Array c/c++ Implementations with a unified interface
- A fast, lightweight, and robust C API library to construct the suffix array